2024年3月20日下午高中数学组全体教师齐聚阶梯教室一参加教研。本次教研由文博高三数学老师高尚主讲。高尚老师讲解了端点效应在近几年数学联考以及高考中的应用。

高尚老师展示联考例题

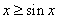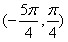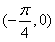首先，高尚老师分享了2020年河北、江苏、辽宁等八个省份的联考压轴导数题。试题的第一问运用放缩法，即当时，成立，将函数的区间分为两部分证明，而另一部分如果用隐零点来证明的话过于麻烦，高老师对函数整体进行分析，考虑函数的有界性及单调性，将区间再分为和进行解决。

试题的第二问高老师运用参变分离法、分类讨论法以及端点效应来进行讲解。其中参变分离的难点，一在于当时，函数值无法取到，要用到洛必达法则。二是当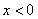时，锐根据第一问的结论很容易进行分类讨论，但当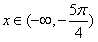时，此时函数的二阶导数的正负因一直发生变化而无法用导数的思想，只能整体考虑用分式思想进行放缩。分类讨论的难点一是分类较难考虑细致，二依旧是当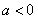时导数无法解决，要考虑用特殊值解决问题。而运用端点效应可以很容易的得出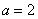，最后进行检验即可，难度骤减。

组内教师认真聆听

最后，高尚老师展示了2020年的新高考1卷21题，借助端点效应可快速得出结果，再加以验证即可。此题还可以用同构的方法构造函数加以解决，2023年的全国甲卷21题也可用端点效应快速解决。

王博老师点评