2022年3月9日下午，高中数学组全体教师齐聚实验楼阶梯教室一参加专题小论坛活动。本次小论坛由数学竞赛教练贾玉明老师主讲。

贾玉明老师为大家分享了关于生成性教学的一些研究成果和个人心得，其围绕高中所学立体几何图形的内切球、棱切球以及外接球问题进行介绍，主要就正方体、正四面体、长方体与球的关系进行教学过程的分析与处理。

对于球与各个立体图形研究的重点就是通过立体图形的边长来求解内接、棱切与外接球的半径。贾玉明老师首先从最简单的正方体与球的关系进行讲解。假设正方体的边长为a,求出内切球半径 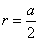,棱切球半径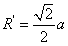以及外接球的半径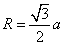。然后通过连接正方体相对两面的异面对角线，就轻松构造了一个正四面体。

紧接着，贾玉明老师通过对边长为a的正四面体和正方体与球的巧妙的联系，求得其外接圆的半径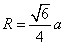，棱切球的半径为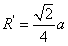，最后通过等体积法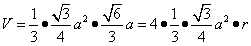，求得其内切球的半径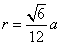，进而知道球心将正四面体的高分为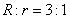，随之运用这个结论可以解决在正四面体内嵌入四个球甚至十个球的竞赛题，贾玉明老师的分析能力与循序渐进的教授方法让大家深感佩服。

最后，贾玉明老师讲述了边长分别为a、b、c的长方体与球的关系，其外接球的半径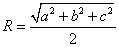。结合我国古代的数学专著《九章算术》，对高中数学中可以放在长方体中解决的的立体图形问题进行论述，如长方体沿不在同一面上的相对两棱斜解所得的立体，即两底面为直角三角形的三棱柱——堑堵；斜切堑堵，四个面均为直角三角形的三棱锥——鳖臑；斜切堑堵，除鳖臑外的另一个立体图形，即底面为长方形，两个三角面与底面垂直的四棱锥体——阳马。贾玉明老师提倡循序渐进的生成性课堂教学模式，让学生更容易接受新知识，也更愿意去探索知识，也使其掌握了学习的方法与乐趣，赢得了大家的阵阵掌声。

在小论坛的最后，由教研组长程建辉老师进行点评，程老师指出，立体结合外接球和内切球的相关计算方法最主要是直接法和构造法，2019年高考第12题和2020年高考第10题对球的相关知识进行了考查，这块内容是高考考查的热点。本次分享贾玉明老师分析到位，直击难点，同时将数学文化融入课堂，值得大家学习。同时呼吁在座各位在教学过程中注意总结和积累，欢迎更多的老师通过小论坛分享经验以共同提高。

（文/高尚）